优化问题
我们工作生活中的很多问题都是优化问题。在本文中,我们给出几个典型的例子,并尝试使用现有的求解器进行求解,作为参照。在后续文章中,我们将介绍一些启发式算法,并对本文中的问题进行求解。
问题1: 离散空间优化问题
luogu P1048 采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 $2$ 个整数 $T$($1 \le T \le 1000, \ 1 \le T \le 000$)和 $M$($1 \le M \le 100, \ 1 \le M \le 100$),用一个空格隔开,$T$ 代表总共能够用来采药的时间,$M$ 代表山洞里的草药的数目。
接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间(包括 $1$ 和 $100$)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入样例
70 3 71 100 69 1 1 2输出样例
3说明
- 对于 30% 的数据,$M \le 10$
- 对于全部的数据,$M \le 100$
这是一个典型的0/1背包问题,我们用$x_{i}$表示第$i$种草药采集与否,用$t_{i}$表示采集第$i$种草药所需要的时间,用$m_{i}$表示第$i$种草药的价值,我们的目标是在有限的时间$T$内使采集到的草药价值最大,那么我们就会得到如下的形式化表述: $$\begin{equation}\label{eq1} \begin{aligned} max \ \sum_{i = 1}^{M} x_{i}m_{i} & \\ x_{i}(x_{i}-1) = 0, i \in [1, M] \\ 0 \le \sum_{i = 1}^{M}{x_{i}t_{i} \le T} \\ \end{aligned} \end{equation}$$
上面公式中的$x_{i}(x_{i-1})=0$是为了确保$x_{i}$只能取0和1。针对这个问题,我们使用如下的程序进行求解:
#!/usr/bin/python3
from scipy.optimize import minimize
from scipy.optimize import SR1
from scipy.optimize import NonlinearConstraint
from scipy.optimize import LinearConstraint
import numpy as np
def solve():
def rosen(x):
"""The Rosenbrock function"""
m = [100, 1, 2] # values
total = 0
for i in range(len(m)):
total = x[i] * m[i]
return -total
# the constraints
def cons_f(x):
return [i * (i - 1) for i in x]
def cons_J(x):
return [[2 * x[0] - 1, 0, 0], [0, 2 * x[1] - 1, 0],
[0, 0, 2 * x[2] - 1]]
def cons_H(x, v):
return v[0] * np.array(
[[2, 0, 0], [0, 0, 0], [0, 0, 0]]) + v[1] * np.array([
[0, 0, 0], [0, 2, 0], [0, 0, 0]
]) + v[2] * np.array([[0, 0, 0], [0, 0, 0], [0, 0, 2]])
nonlinear_constraint = NonlinearConstraint(cons_f, [0, 0, 0], [0, 0, 0],
jac=cons_J,
hess=cons_H)
linear_constraint = LinearConstraint([[71, 69, 1]], [0], [70])
x0 = [1, 0, 0]
res = minimize(rosen,
x0,
method='trust-constr',
jac="2-point",
hess=SR1(),
constraints=[nonlinear_constraint, linear_constraint],
options={'verbose': 1})
print(res)
if __name__ == "__main__":
solve()
输出结果:
barrier_parameter: 2.048000000000001e-09
barrier_tolerance: 2.048000000000001e-09
cg_niter: 0
cg_stop_cond: 1
constr: [array([-0.0073379 , 0.00693036, 0.0001018 ]), array([70.00010182])]
constr_nfev: [106, 0]
constr_nhev: [82, 0]
constr_njev: [79, 0]
constr_penalty: 1.0
constr_violation: 0.0073378956828978265
execution_time: 0.149078369140625
fun: 0.00020358301622653028
grad: array([ 0., -0., -2.])
jac: [array([[ 0.98521491, 0. , 0. ],
[ 0. , -1.01376596, 0. ],
[ 0. , 0. , -1.00020358]]), array([[71, 69, 1]])]
lagrangian_grad: array([-7.48012763e-15, -1.15411153e-14, -2.22470154e-15])
message: '`xtol` termination condition is satisfied.'
method: 'tr_interior_point'
nfev: 424
nhev: 0
nit: 188
niter: 188
njev: 106
optimality: 1.1541115285673698e-14
status: 2
success: True
tr_radius: 1.0000000000000005e-09
v: [array([-0.01465935, 0.01384519, -1.99938954]), array([0.00020342])]
x: array([ 9.92607455e-01, -6.88298061e-03, -1.01791508e-04])
可以看到使用这个求解器并没有得到正确的结果,上面提到的二值约束对这个求解器不是很友好,求解的结果也不满足约束条件。
问题2: 连续空间多变量多约束非线性规划问题
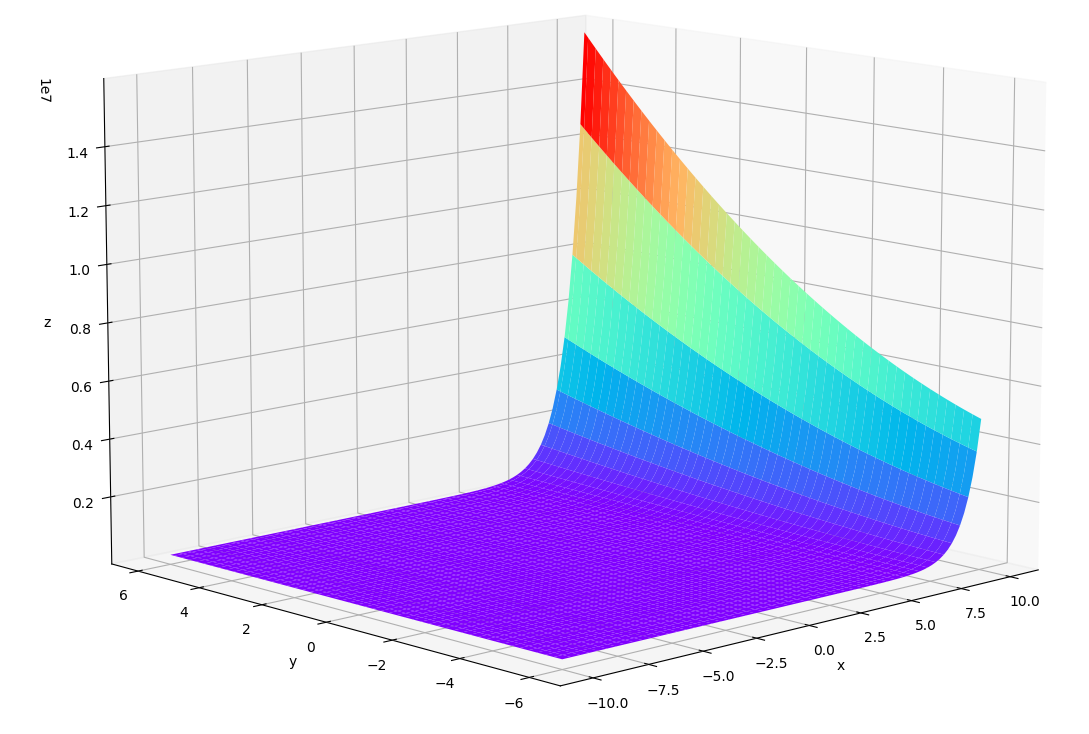
$$min \ f(x) = e^{x_{1}}(4x_{1}^{2}+2x_{2}^{2}+4x_{1}x_{2}+2x_{2}+1)$$
$$\begin{equation}\label{eq2} \begin{aligned} 1.5 + x_{1}x_{2} -x_{1} - x_{2} &\leq 0 \\ -x_{1}x_{2} &\leq 10 \\ -10 \leq x_{1} &\leq 10 \\ -6 \leq x_{2} &\leq 6 \\ \end{aligned} \end{equation}$$
我们先来看一下函数图像,基本上$x, y$越小,函数的值越小。
我们使用下面的程序对这个问题进行求解:
#!/usr/bin/python3
import math
from scipy.optimize import Bounds
from scipy.optimize import minimize
from scipy.optimize import SR1
from scipy.optimize import NonlinearConstraint
import numpy as np
import matplotlib.pyplot as plt
def plot():
def f(x, y):
return np.exp(x) * (4 * x * x + 2 * y * y + 4 * x * y + 2 * y + 1)
x = np.linspace(-10, 10, 100)
y = np.linspace(-6, 6, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, cmap='rainbow')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
plt.tight_layout()
def solve():
def rosen(x):
"""The Rosenbrock function"""
return math.exp(x[0]) * (4 * x[0] * x[0] + 2 * x[1] * x[1] +
4 * x[0] * x[1] + 2 * x[1] + 1)
# the bound
bounds = Bounds([-10.0, -6.0], [10.0, 6.0])
# the constraints
def cons_f(x):
return [1.5 + x[0] * x[1] - x[0] - x[1], -x[0] * x[1]]
def cons_J(x):
return [[x[1] - 1, x[0] - 1], [-1, -1]]
def cons_H(x, v):
return v[0] * np.array([[0, 1], [1, 0]]) + v[1] * np.array([[0, -1],
[-1, 0]])
nonlinear_constraint = NonlinearConstraint(cons_f, [-np.inf, -np.inf],
[0, 10],
jac=cons_J,
hess=cons_H)
x0 = [0.0, 5.0]
res = minimize(rosen,
x0,
method='trust-constr',
jac="2-point",
hess=SR1(),
constraints=[nonlinear_constraint],
options={'verbose': 1},
bounds=bounds)
print(res)
if __name__ == "__main__":
plot()
solve()
输出结果:
barrier_parameter: 2.048000000000001e-09
barrier_tolerance: 2.048000000000001e-09
cg_niter: 529
cg_stop_cond: 2
constr: [array([-1.82051237, 9.73411463]), array([-7.68091424, 1.26731198])]
constr_nfev: [564, 0]
constr_nhev: [289, 0]
constr_njev: [288, 0]
constr_penalty: 1.0
constr_violation: 0.0
execution_time: 0.5691990852355957
fun: 0.0940626469286803
grad: array([ 0.06804119, -0.01091776])
jac: [array([[ 0.26731198, -8.68091424],
[-1. , -1. ]]), array([[1., 0.],
[0., 1.]])]
lagrangian_grad: array([ 0.00747274, -0.00263313])
message: '`xtol` termination condition is satisfied.'
method: 'tr_interior_point'
nfev: 1692
nhev: 0
nit: 536
niter: 536
njev: 564
optimality: 0.007472736269283172
status: 2
success: True
tr_radius: 6.8134308785272305e-09
v: [array([-0.00751795, 0.05714546]), array([-0.00141336, 0.00016742])]
x: array([-7.68091424, 1.26731198])
初步验证一下,这个结果应该是符合预期的。
问题3: 连续空间最值问题
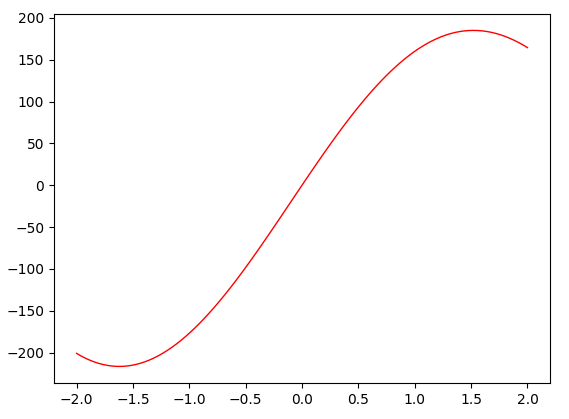
$$\begin{equation}\label{eq3} \begin{aligned} max \ f(x) = 200&e^{-0.05x}sin(x) \\ -2 \le &x \le 2 \end{aligned} \end{equation}$$
我们先来看一下函数图像,这个结果比较明显.
针对这个问题,我们使用如下的程序进行求解:
#!/usr/bin/python3
import math
from scipy.optimize import Bounds
from scipy.optimize import minimize
from scipy.optimize import SR1
import numpy as np
import matplotlib.pyplot as plt
def rosen(x):
"""The Rosenbrock function"""
return -200 * math.exp(-0.05 * x) * math.sin(x)
def plot():
x = np.linspace(-2, 2, 100)
y = [rosen(i) for i in x]
plt.plot(x, y, color="r", linestyle="-", linewidth=1)
plt.show()
def solve():
bounds = Bounds([-2.0], [2.0])
x0 = [0]
res = minimize(rosen,
x0,
method='trust-constr',
jac="2-point",
hess=SR1(),
options={'verbose': 1},
bounds=bounds)
print(res)
if __name__ == "__main__":
plot()
solve()
输出结果:
barrier_parameter: 3.200000000000001e-05
barrier_tolerance: 3.200000000000001e-05
cg_niter: 9
cg_stop_cond: 1
constr: [array([1.52083761])]
constr_nfev: [0]
constr_nhev: [0]
constr_njev: [0]
constr_penalty: 1.0
constr_violation: 0.0
execution_time: 0.08674049377441406
fun: -185.1242145731396
grad: array([-5.76906021e-05])
jac: [<1x1 sparse matrix of type '<class 'numpy.float64'>'
with 1 stored elements in Compressed Sparse Row format>]
lagrangian_grad: array([7.09417522e-10])
message: '`gtol` termination condition is satisfied.'
method: 'tr_interior_point'
nfev: 20
nhev: 0
nit: 15
niter: 15
njev: 10
optimality: 7.0941752157368e-10
status: 1
success: True
tr_radius: 24107.414128166944
v: [array([5.76913115e-05])]
x: array([1.52083761])
根据图像得知,这个求解结果是正确的。
参考资料
- https://cloud.tencent.com/developer/article/1099730
- https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html